Định Nghĩa Hàm Tuyến Tính: Tổng Giá Trị Của Khái Niệm Này
Hàm tuyến tính là một trong những khái niệm cơ bản, được sử dụng rộng rãi trong toán học và các lĩnh vực khoa học khác. Định nghĩa hàm tuyến tính tổng giá trị của khái niệm này thể hiện một cách đầy đủ về tính chất và ứng dụng, giúp lý giải các mối quan hệ tuyến tính thông qua đồ thị là một đường thẳng. Hãy cùng Truemen tìm hiểu chi tiết trong bài viết này nhé!
1. Định Nghĩa Hàm Tuyến Tính Tổng Giá Trị Của Khái Niệm Này
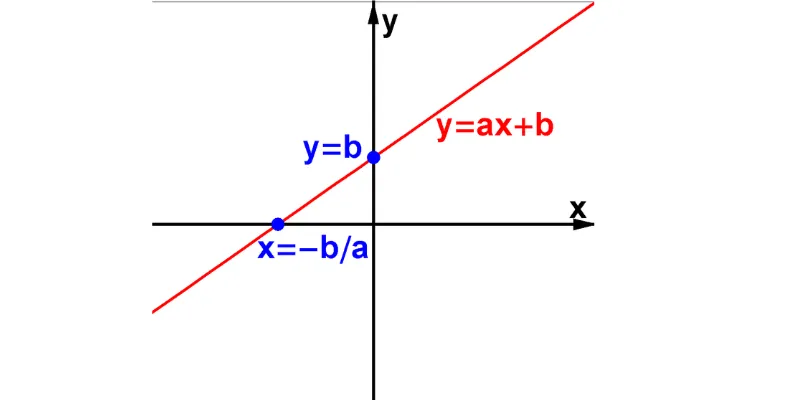
Hàm tuyến tính có dạng: f(x)=mx+b
Trong đó:
- m: Hệ số góc (độ dốc), biểu thị tốc độ thay đổi của hàm.
- b: Giao điểm với trục y, thể hiện giá trị của hàm khi x=0.
Định nghĩa hàm tuyến tính tổng giá trị của khái niệm này bao gồm hai tính chất chính:
- Tính cộng tính: f(x+y)=f(x)+f(y).
- Tính đồng biến: f(αx)=αf(x), với α là số thực.

2. Tổng Giá Trị Của Hàm Tuyến Tính Trong Các Lĩnh Vực
2.1. Trong Toán Học
Hàm tuyến tính là công cụ không thể thiếu để giải quyết các vấn đề toán học. Định nghĩa hàm tuyến tính tổng giá trị của khái niệm này đặc biệt hữu ích trong:
- Biểu diễn mối quan hệ tỉ lệ thuận giữa các đại lượng.
- Giải các phương trình tuyến tính hoặc ánh xạ không gian vector.
Ví dụ: Hàm y=2x+5 là một hàm tuyến tính, với hệ số góc m=2 và giao điểm b=5.
2.2. Trong Vật Lý
- Mô tả hiện tượng tự nhiên qua các phương trình vi phân tuyến tính, như:
- Phương trình Maxwell: Biểu diễn sóng điện từ.
- Phương trình khuếch tán: Mô tả quá trình truyền nhiệt hoặc lan truyền hạt.
2.3. Trong Điện Tử
- Khuếch đại tuyến tính: Duy trì hình dạng tín hiệu đầu ra tương ứng với đầu vào.
- Bộ lọc tuyến tính: Loại bỏ tạp âm nhưng không làm thay đổi đặc tính tín hiệu.
2.4. Trong Nghệ Thuật
- Phong cách tuyến tính được ứng dụng trong hội họa thời Phục hưng, nơi các chi tiết được phác thảo rõ ràng bằng đường nét.
- Trong âm nhạc, tuyến tính thể hiện qua sự kế thừa giữa các nốt nhạc trong một giai điệu.
2.5. Trong Đời Sống Hàng Ngày
Hàm tuyến tính còn thể hiện ở những khía cạnh thực tế như:
- Mối quan hệ tỉ lệ trong đo lường (chiều dài tuyến tính).
- Hiệu suất của các hệ thống máy móc.
3. Lợi Ích Của Định Nghĩa Hàm Tuyến Tính
Định nghĩa hàm tuyến tính tổng giá trị của khái niệm này không chỉ giúp giải các bài toán học thuật mà còn mở rộng ứng dụng trong nhiều lĩnh vực khác.Hiểu rõ định nghĩa hàm tuyến tính tổng giá trị của khái niệm này giúp bạn:
- Tăng khả năng tư duy logic và phân tích.
- Dễ dàng giải các bài toán phức tạp.
- Ứng dụng linh hoạt trong công việc và nghiên cứu.

Xem thêm: Các dạng toán nâng cao lớp 3.
4. Kết Luận
Định nghĩa hàm tuyến tính tổng giá trị của khái niệm này là nền tảng vững chắc để bạn hiểu rõ các hiện tượng trong tự nhiên, ứng dụng công nghệ và cuộc sống, là chìa khóa để hiểu các nguyên tắc cơ bản của toán học và ứng dụng thực tiễn. Việc nắm bắt rõ ràng và áp dụng hiệu quả sẽ mang lại nhiều lợi ích trong học tập, nghiên cứu và thực tiễn. Hãy đầu tư thời gian để làm chủ khái niệm quan trọng này ngay hôm nay!